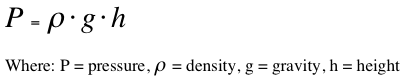Have you ever wondered why silos are generally tall and slender while oil tanks are short and squat? Take a look at the two images below…compare the height-to-diameter ratios for the different vessels.
So, why do you typically see silos/bins/tanks for powders and bulk solids with tall and slender cylinders, while for liquids we generally find the cylinder is short and squat? The answer lies within the simple equation below for uniform hoop stress (θs) for a cylinder.
Hoop stress is calculated from knowing the internal pressure exerted against the vessel wall, the diameter of the cylinder, and the cylinder thickness. As shown above, the hoop stress is proportional to both cylinder diameter and internal pressure, while inversely proportional to wall thickness.
A very important component in the equation above is the pressure (P). How should this be estimated for a tank holding a liquid? This is a straight forward calculation; the pressure in liquid tank is equal to the product of the liquid’s density, column height, and gravity, as shown in the equation below.
Therefore, as the liquid tank gets larger, either with its diameter or its column height, the wall thickness must increase to avoid exceeding the allowable hoop stress for the wall material of construction. This is why we see liquid tanks short and squat; the pressure from the liquid goes up proportionally with height, thereby requiring the wall thickness increase to go up at the same rate. This approach quickly increases the cost of the tank, its foundation, and supports.
But, can we use this expression to calculate the pressure for a bulk solid? The answer is…absolutely not, except for one condition where the bulk material (a powder) is in a fully fluidized (i.e., liquid) state. Proven methods are used by Jenike & Johanson for calculating the material-induced loads in a silo, bin, and hopper.
The key is that though hoop stress is required for analysis of the thin-shelled vessel, the effects of particle shear forces along the interior walls must also be analyzed to assess buckling stresses. Herein we see a condition not experienced by liquids during storage. With liquids, their shear force is zero when the material does not move (Newton’s law of viscosity), whereas with bulk solids, the shear force is non-zero and can be a significant amount during both storage and discharge from the vessel.
You have probably experienced this effect if you ever tried to pull a fence post out of the ground; even in free-flowing, dry sand, the bulk solid exerts shear forces against the post resisting your efforts to extract it from the ground.
This interior shear force on the vessel wall requires sufficient wall reinforcement to avoid wall buckling, but, it also is highly beneficial in limiting the vertical load transmission from a column of bulk material. This was determined experimentally and defined from first-principles mathematically by Janssen [1] in the late 19th century — to this date Janssen’s distribution is the basis for all silo design codes.
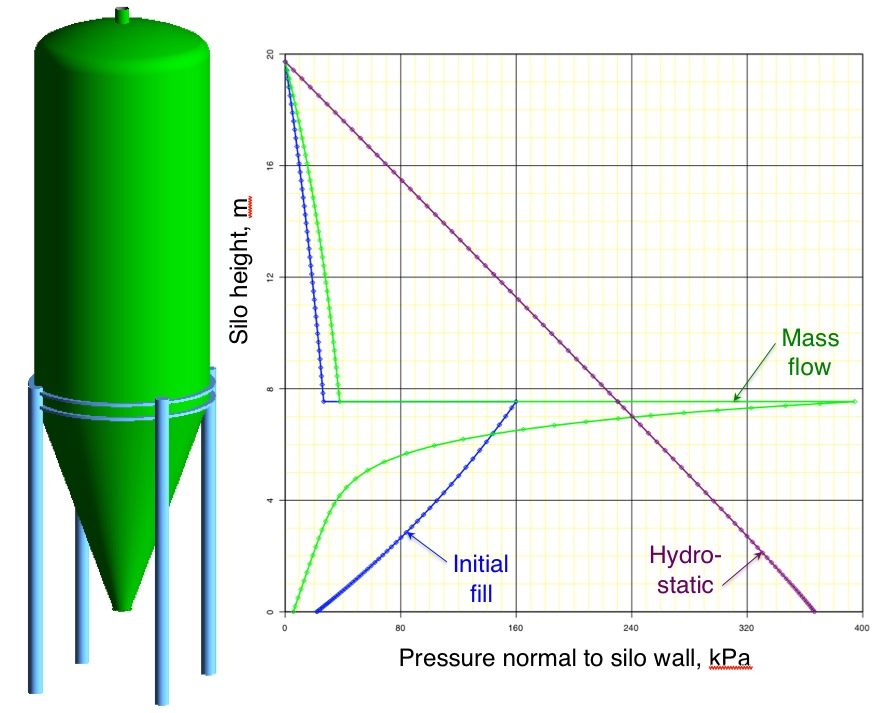
Janssen’s formulation shows in general that when a vessel’s height-to-diameter ratio exceeds three, any additional pressure added to the top of the bulk solid column does not significantly increase the pressures at the column base. In other words, the pressure in the column has an asymptotic behavior, as shown in the figure below. Compare the pressures for a liquid vs. a bulk solid in a tank (for both mass flow and initial fill/funnel flow conditions). With this graph alone, one can easily understand why we see tall and slender silos/bins/tanks for powders and bulk solids, while for liquids we generally find the tank is short and squat.
[1] Janssen, V.H.A., “Versuche über getreidedruck in silozellen”, Zeitschrift es Vereines Deutsher Ingenieure, 39 (1895), 1045-1049.